Most of the folks among us would have heard of the terms "encryption" , "security" , "safety" etc. and these mostly refer to the cybersecurity principles which have become the norm in today's information world where data has become a traceable entity. Dare I say, Data is the new oil as per many people over the internet.
But even then, we tend to not pay much attention to the concept of data integrity.
What? Data integrity is different than encryption?
The answer is yes. Encryption refers to the security principle that when 2 people are communicating then it should be extremely difficult or a one in a trillion stroke of extremely good luck for an eavesdropper to read the messages and make sense of it. Whereas, data integrity refers to the principle that if you received a photo from a good friend of yours, you should be pretty relaxed and not go on a freak trip thinking someone might have sent you a different photo and you can't tell the difference.
But won't encrypting the photo solve our problem?
Well, yes and no. The way modern public key cryptography works, it can't be used as a means of data integrity on its own. But we can use a combination of public key cryptography and a cryptographic hash function to achieve data integrity. But I will leave this part for a separate article.
Cryptographic hash function? Why are you throwing buzzwords on us?
Well cryptographic hash functions are not buzzwords. They are an integral (pun intended) part of modern security practices. All they do is take in some input and give some output but they need to follow some more properties. Let's denote the function using H , H(x) = y. Here, x is the input and y is the output. We will refer to the output as digest. A cryptographic hash function has the following properties:
- same input should always return the same output. H(x) = H(x') when x = x'
- it should be computationally infeasible to determine the input from the output. finding x from y is not feasible.
- it should be computationally infeasible to find out another input which returns the same output. if we know x and H(x) = y, then finding another x' != x such that H(x') = H(x) should be computationally infeasible.
There are a bunch of cryptographic hash functions being used nowadays. I have added some references at the end of this article for further reading.
So what is a Merkle Tree, the title of this article?
Patience my young padawan, we should first understand how are cryptographic hash functions being used to achieve data integrity. Let's take a situation where Bob has a document sent to Alice for her to e-sign. Alice signs it and after that Bob changes one value in the document. Now, Alice has no proof to say that Bob did something fishy. Here come our good friends cryptographic hash functions to help Alice. Both Alice and Bob calculate the digest of the document using an agreed upon hash function and exchange the digest with each other to establish that they are both viewing the same document. Now, if someone changes anything in the document, the digest for the same will change and the other person can say that something has changed.
Okay, so our data integrity problem is solved. Hurray.
Well, not so much. It is possible that the hash function used was quite weak and Bob was somehow able to change the document and even maintain the same digest as the original one. To solve this problem, we introduce Merkle trees into the picture.
Finally, Merkle trees. How do they help us with data integrity?
in summary, instead of calculating the digest of the document in one shot. We convert the document into a byte array. Then split it into several slices.
For each slice, we calculate the digest of that slice. The resultant digests are treated as the leaf nodes of a binary tree. Then we go on to construct the binary tree in a bottom-up fashion using a simple algorithm which is stated next.
parent node = *H(left child + right child)*
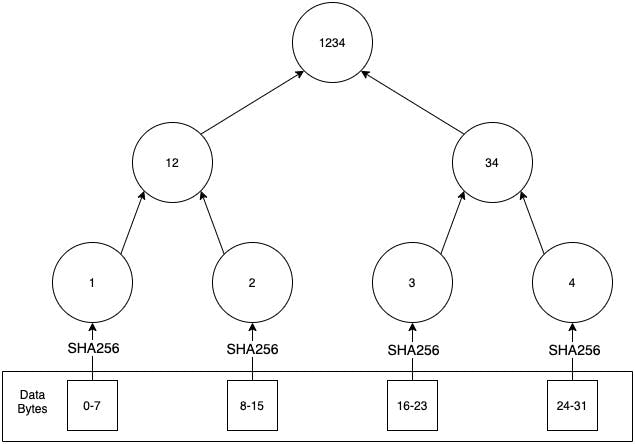
Ultimately, the root node denotes the digest of the entire document.
Okay, I understand how Merkle tree is constructed but how does it help with data integrity?
If we recall the properties of cryptographic hash functions it should be computationally infeasible to find out another input which returns the same output. To somehow change the content of the document without changing the digest at the lowest level is going to be extremely difficult, someone needs a spectacular alignment of stars and planets to pull off something like that.
More so if someone tries some funny business, we can actually pinpoint in which slice of data was the aforementioned change done, we can see how to do it with the help of the below diagram.
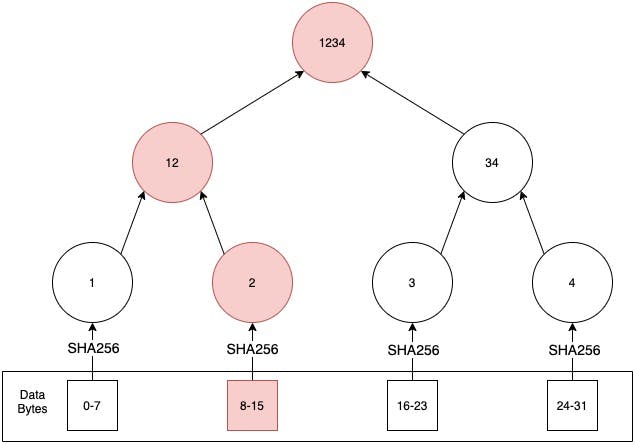
We can see that a change in the 2nd slice causes the digest to change all the way to the root. So we can compare the two merkle trees and narrow down on the changed block by comparing the path from root node to leaf nodes. We move down the path where we find the digest to be differing from the previously constructed merkle tree.

To start looking into a sample code for Merkle tree generation and verification, we will first generate some random data and write it into a file.
For our example we will generate an array of integers, for that we will first specify the numbers of integers we will generate and also the height of the tree.
const (
size = 4096
treeLevels = 4
)
Now we define a function to generate the random integers and write it into a file.
func generateFileData(){
data := make([]int,size) // array of random integers
for i:=0;i<size;i++ {
n := rand.Int()
data[i] = n
}
file, err := os.OpenFile("./data.txt", os.O_CREATE|os.O_RDWR|os.O_TRUNC, os.ModePerm)
if err != nil {
fmt.Println(err)
return
}
file.Truncate(0) //erasing contents of the file
file.Seek(0,0) //moving write cursor to the start of file
defer func(){
if clErr := file.Close(); clErr!=nil {
fmt.Println(clErr)
}
}()
bytes,_ := json.Marshal(data) // converting array to bytes
_, err = file.Write(bytes) // writing bytes to file
if err!=nil {
fmt.Println(err)
}
}
Now to generate the Merkle tree, we will read the data from the file and store it into an integer array.
func readDataFile() []int {
data := make([]int,size)
text, err := os.ReadFile("./data.txt")
if err!=nil {
fmt.Println(err)
}
json.Unmarshal(text,&data) //reading bytes to integer array
return data
}
Now we will write the code to generate the tree, but before that we will define the struct of the tree node and a Constructor function to return a node.
type MerkleTree struct{
Data string `json:"data"`
Left *MerkleTree `json:"left,omitempty"`
Right *MerkleTree `json:"right,omitempty"`
}
func NewMerkleTreeNode() *MerkleTree {
return &MerkleTree{}
}
We will now define the driver function which will actually generate the tree and write the tree data as a JSON in a file.
func generateTree(data []int){
startTime := time.Now()
root := NewMerkleTreeNode() //root node of merkle tree
createTree(root, 0,len(data),treeLevels,data)
endTime := time.Now()
//to display time taken in generating the tree
fmt.Println(startTime,endTime,endTime.Sub(startTime).Microseconds())
savetoFile(root) //function to save the tree into a file
}
Now our recursive function to create the tree.
func createTree(root *MerkleTree, start, end, level int, data []int) {
if level==0 {
bytes, _ := json.Marshal(data[start:end])
hash := sha256.Sum256(bytes)
root.Data = fmt.Sprintf("%x",hash)
return
}
root.Left = NewMerkleTreeNode()
root.Right = NewMerkleTreeNode()
mid := (start+end)/2 //splits the array into 2 parts
createTree(root.Left,start,mid+1,level-1,data) //left sub-array
createTree(root.Right,mid+1,end,level-1,data) //right sub-array
rootHash := sha256.Sum256([]byte(root.Left.Data+root.Right.Data)) //concatenating children's digest and creating a new digest.
root.Data = fmt.Sprintf("%x",rootHash) //converting byte array to string
}
Function to save the tree into a JSON file.
func savetoFile(root *MerkleTree) {
file, err := os.OpenFile("./tree.json", os.O_CREATE|os.O_RDWR|os.O_TRUNC, os.ModePerm)
if err != nil {
fmt.Println(err)
return
}
file.Truncate(0)
file.Seek(0,0)
defer func(){
if clErr := file.Close(); clErr!=nil {
fmt.Println(clErr)
}
}()
bytes,_ := json.Marshal(root)
_, err = file.Write(bytes)
if err!=nil {
fmt.Println(err)
}
}
We have written the code to generate the Merkle tree and write it into a JSON file.
Next, we will look into verifying a file for data integrity. For this step, we write a driver function to read the file data and also read the previously generated merkle tree from the files.
func verifyMerkleTree() {
prevTree := NewMerkleTreeNode()
text, err := os.ReadFile("./tree.json") //reading previously created merkle tree
if err!=nil {
fmt.Println(err)
}
json.Unmarshal(text,prevTree) //unmarshal merkle tree into the struct
data := readDataFile() //reading random data generated
root := NewMerkleTreeNode()
createTree(root, 0,len(data),treeLevels,data) //creating merkle tree again from the recently read data from the file
startTime := time.Now()
verifyTree(prevTree, root, 0, len(data)) //function to compare the previous and current trees
endTime := time.Now()
//monitoring how much time it took to compare the two trees.
fmt.Println(startTime,endTime,endTime.Sub(startTime).Microseconds())
}
The function which compares the previous tree with the current tree and helps verify if the data integrity has actually been maintained or not.
func verifyTree(prevTree, root *MerkleTree, start, end int) {
if prevTree==nil && root==nil {
return
}
if prevTree==nil || root==nil {
fmt.Printf("Error, prevTree: %+v, root: %+v",prevTree,root)
return
}
if prevTree.Data==root.Data {
return
}
fmt.Printf("Difference found: start: %d, end: %d, prevTree.Data: %s, root.Data: %s\n",start, end, prevTree.Data, root.Data)
mid := (start+end)/2
verifyTree(prevTree.Left, root.Left, start,mid)
verifyTree(prevTree.Right, root.Right, mid,end)
}
References:
